acvilla.blogg.se - To regress x on y

Another example is when one is plotting Y/X against X - for example some weight specific function against an organism's body weight. In this case the spurious correlation tends to be positive. Pearson (1897) was the first to note that two variables having no correlation between themselves become correlated when divided by a third uncorrelated variable. For example two variables (X and Y) may be standardized by dividing by a third variable (Z), and Y/Z is then regressed on X/Z. One common reason for two variables not being independent is when they share a common term. There is, however, general agreement that one cannot use the usual parametric tests of significance in this situation. Prairie & Bird (1989) on the other hand argue that it is not the correlations that are spurious, but the inferences drawn from them. It has been suggested that erroneous conclusions derived from spurious correlations may be more widespread and persistent in the literature than pseudo-replication ever was. This has come to be known as the 'spurious correlation' issue. If the dependent and independent variables, Y and X, are not independent, then regression or correlation analysis may well indicate they are correlated when in fact the relationship derives solely from the presence of a shared variable. This is a controversial topic which has generated considerable debate in the journals. SE b is the standard error of the slope.t is a quantile from the t-distribution for the chosen type I error rate (α) and n-2 degrees of freedom,.b is the slope of the regression of Y on X,.However, the confidence interval of this estimate is rather tedious to obtain as it requires computation of two further statistics, commonly known as D and H.

b is the slope and a is the intercept of the regression on Y on X.

This method is unbiased providing the usual assumptions of regression are met - in particular that X is measured without error.Īn unbiased estimate of X ( ) for a specified Y value (Y p) is obtained simply by reversing the equation. Instead one should use the method of inverse regression. If the X values are fixed and measured without error, it would not be valid to simply regress X on Y rather than vice versa as the assumptions of regression would not be met. Sometimes we may need to estimate X from Y, rather than the more usual procedure of estimating Y from X.

n is the number of bivariate observations, and m is the number of replicates for the predicted mean.

X p is the value of X for which Y is being estimated or predicted,.

MS error is the mean square error which is Σ(Y − ) 2/ (n− 2) where is the expected value of Y for each value of X,.

The error sums of squares is obtained by subtracting the regression sums of squares from the total sums of squares. The total sums of squares of the response variable (Y) is partitioned into the variation explained by the regression and the unexplained error variation. If errors are not normally and identically distributed, then a randomization test should be used. Analysis of variance is often the preferred approach, although one can also use a t-test to test whether the slope is significantly different from zero. Providing errors are normally and identically distributed, a parametric test can be used.

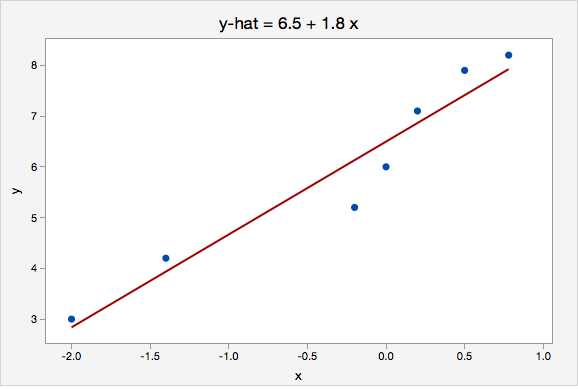
There are several ways the significance of a regression can be tested. a is the estimate of the Y intercept (α ) (the value of Y where X=0).n is the number of bivariate observations.X and Y are the individual observations,.b is the estimate of the slope coefficient (β ),.The parameters of the regression model are estimated from the data using ordinary least squares. Errors on the response variable are assumed to be independent and identically and normally distributed. If there is substantial measurement error on X, and the values of the estimated parameters are of interest, then errors-in-variables regression should be used. The model is still valid if X is random (as is more commonly the case), but only if X is measured without error. In the traditional regression model, values of X-variable are assumed to be fixed by the experimenter. Where β 0 is the y intercept, β 1 is the slope of the line, and ε is a random error term. Where α is the y intercept (the value of Y where X = 0), β is the slope of the line, and ε is a random error term. This is in contrast to correlation where there is no distinction between Y and X in terms of which is an explanatory variable and which a In classical (or asymmetric ) regression one variable (Y) is called the response or dependent variable, and the other (X) is called the explanatory or independent variable. Simple linear regression provides a means to model a straight line relationship between two variables.